Leetcode – 17. Letter Combinations of a Phone Number

Problem

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.

A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

Example 1:

Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]

Solution

Brute force

My idea is:
1. Looping through the digits. At every loop, we check the numToChars array and loop through it.
2. At each loop, we copy the result array and add the specific char at the end.

var letterCombinations = function(digits) {
    let result = [];
    const numToChars = {
        2: ['a', 'b', 'c'],
        3: ['d', 'e', 'f'],
        4: ['g', 'h', 'i'],
        5: ['j', 'k', 'l'],
        6: ['m', 'n', 'o'],
        7: ['p', 'q', 'r', 's'],
        8: ['t', 'u', 'v'],
        9: ['w', 'x', 'y', 'z']
    }
    
    for (let i = 0; i < digits.length; i++) {
        if (i === 0) {
            result = numToChars[digits[i]];
            continue;
        }

        let temp = [];
        for (let j = 0; j < numToChars[digits[i]].length; j++) {
            for (let k = 0; k < result.length; k++) {
                temp.push(result[k] + numToChars[digits[i]][j]);
            }
        }
        result = temp;
    }

    return result;
};

It runs well but it’s not beautiful.

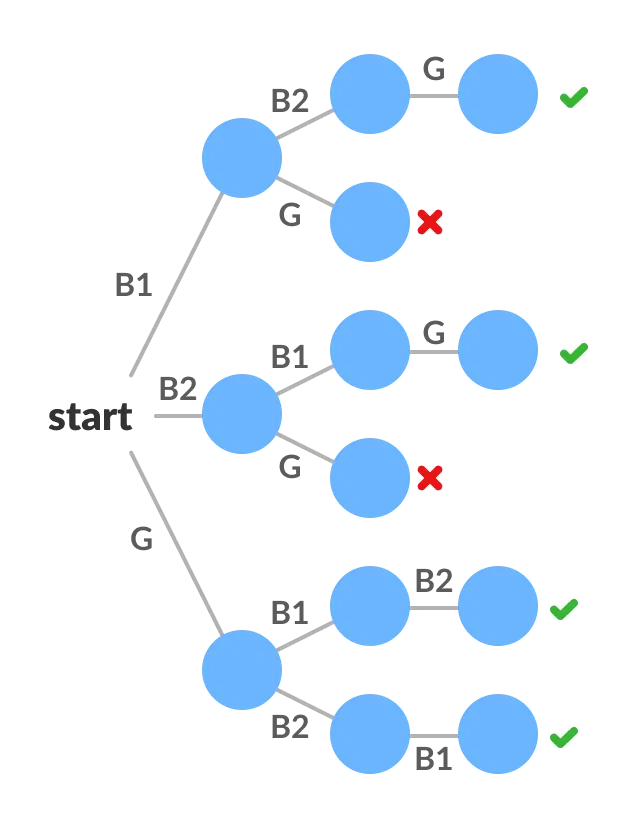
Backtracking technique

Backtracking is a general algorithmic technique used to find solutions to problems by exploring possible candidates, discarding those that cannot lead to a solution, and then backtracking to explore other options.

• Incremental Solution Building: Backtracking algorithms build solutions incrementally, meaning they start with an initial state and gradually add elements or choices to form a potential solution. 
• Constraint Satisfaction: Backtracking is particularly effective for problems where solutions must satisfy certain constraints. 
• Exploration and Abandonment: The algorithm explores different paths or choices, but if a path is found to be invalid or cannot lead to a valid solution, it abandons that path and backtracks to a previous state to explore other possibilities. 
• Depth-First Search: Backtracking often employs a depth-first search approach, meaning it explores one path deeply before backtracking to explore other branches. 
• Brute-Force Approach: At its core, backtracking is a brute-force approach, meaning it explores all possible solutions or candidates until a valid solution is found or all possibilities have been exhausted. 
• Common Applications: Backtracking is used in various problems, including constraint satisfaction problems, pathfinding (like maze solving), and combinatorial problems. 
• Example: Imagine solving a maze. A backtracking algorithm would start at the entrance, move step-by-step towards the exit, and if it reaches a dead end, it would backtrack to the last unvisited branch to explore other paths. 

function letterCombinations(digits) {
  if (!digits.length) return [];

  const phoneMap = {
    '2': 'abc',
    '3': 'def',
    '4': 'ghi',
    '5': 'jkl',
    '6': 'mno',
    '7': 'pqrs',
    '8': 'tuv',
    '9': 'wxyz'
  };

  const result = [];

  function backtrack(index, current) {
    if (index === digits.length) {
      result.push(current);
      return;
    }

    const letters = phoneMap[digits[index]];
    for (let letter of letters) {
      backtrack(index + 1, current + letter);
    }
  }

  backtrack(0, '');
  return result;
}

The code is more simple and beautiful, right?